Mathemagics

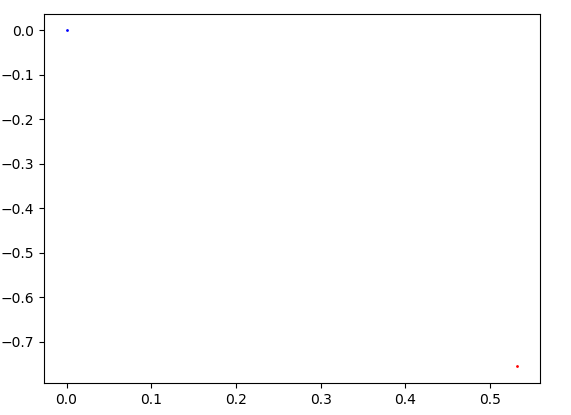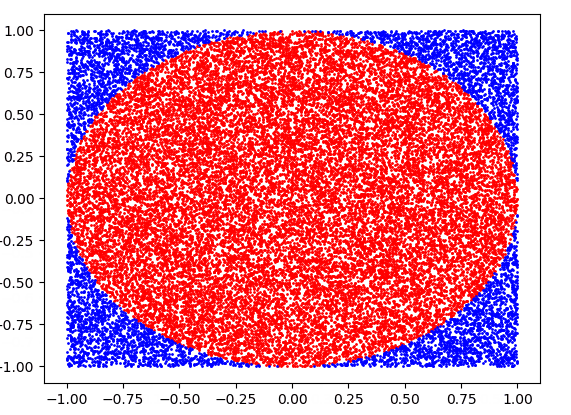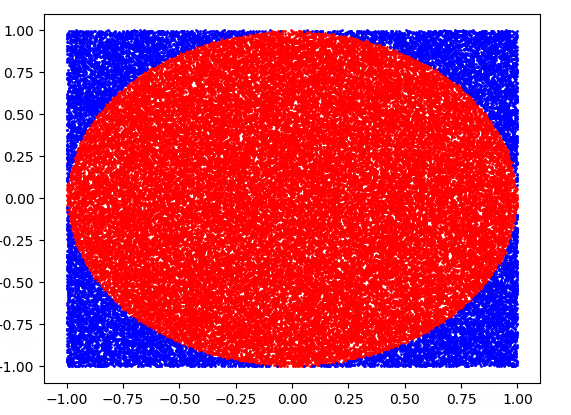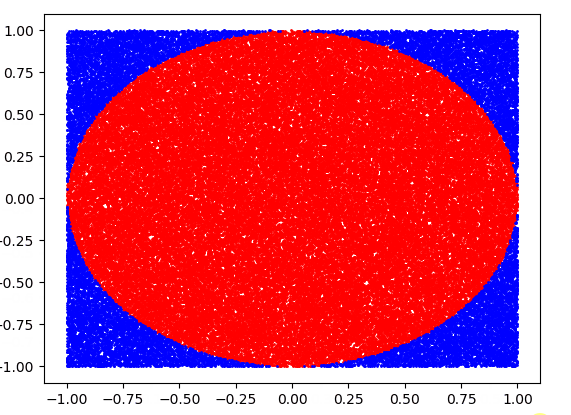
In this short project, I estimate Pi using the Monte Carlo Method. For the uninitiated in the world of mathematics, this means the value of Pi will be brute forced. How? Well, I'm glad you asked. All we need to brute force is to get Pi into an form that we can work with

If we image a circle of radius r inscribed in a square of width 2r then we have all we need. If we think about randomly throwing darts at this figure we should expect a certain portion of them to land inside the circle, another portion of them to land outside the circle but inside the square, and another (hopefully smaller) portion to land outside the square. By looking at the proportion of darts that land inside the circle vs outside the circle but inside the square we can approximate Pi!

It's geometry

How does Pi relate to the ratio of these two areas? Great question. We know the equation to calculate the area of a square; 2 x r. We also know the equation to calculate the area of a circle; 2 x Pi^2 . We can re-arrange these values to get:

This means that if we randomly throw darts at this target and look at the number of darts that landed in each section we can approximate Pi. Next we'll see how accurate this approximation is

Maybe, sort of, kinda of Pi

We can see that at first, the approximation of pi is very poor. But as we increase the number of throws we can see the value starts to converge. We also get a bit of diminishing returns as the number of trials increases but we can get a prett good approximation using only brute force!

For a closer look at the code that generated these plots checkout my github page. This project specifically is linked here