Code

The Mathematica code is set up to let the user explore different betting strategies and game configurations. The user can modify variables like bankroll, minimum and maximum bet, rouletty style, etc. The default values are numbers that I have seen in most casino games (except for the bank roll amount, I haven't seen much of that). The live plot view feature works well with trials under 1000 but times out if evaluation takes too long. To model the spin of a roulette wheel I describe each spin as a binomially distributed (result is win or lose), independent event. The probability of success of depends on the type of bet and the type of roulette table- the European tables have one 0 and the American tables have two 0's!. A random rumber is generated based on the odds of the particular bet and a -1 is returned if the bet results in a loss and a bet multiplier is returned if the bet is succesful. You can get the full code here: https://github.com/arturju/rouletteMonteCarlo

Random betting strategy

To do a model validation we can analytically solve for the expected value of betting black or red. Using a minimum bet of $5 we get: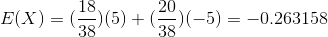

This means that in the long run, if we bet $5 on either black or red we should expect to lose $0.26 per bet. This concept of expected value will help us make some conclusions about other betting methods. We can also see that the curve closely resembles a normal distribution. The more games we play the closer the curve should be to a normal distribution.

Double down strategy

This strategy calls for doubling your initial bet everytime there is a loss and going back to the minimum bet size when there is a win. This would be a somewhat sound strategy if it were not for the maximum bet limits most casinos have on roulette. In this simulation the max bet is capped at $1,000 and it takes a player 7 losses in a row to be unable to double the next bet. This inability to continue doubling our bet becomes the downfall of this strategy in the long run as we can see from the simulation results. In the short term (<~20 bets) however, this strategy seems to have a high change of positive returns but still a negative expected value.